Being interested (on amateur level) in both archaeology and simulations, it was just a matter of time to run into the multi-agent programmable modeling environment NetLogo that is authored by Uri Wilensky and developed at the Northwestern’s Center for Connected Learning and Computer-Based Modeling CCL. The direct reason was the announcement of the online course Modelling and Simulation in Archaeology by Fulco Scherjon (Leiden University), Iza Romanowska (Barcelona Supercomputing Center) and Karsten Lambers (Leiden University).
From the NetLogo website two versions are (freely) available: a desk-top version and a web version. I have little experience with the web version. When I tried to run a desk-top model that use the table extension, I got a message that extensions are not (yet) supported in the web version. However an earlier model without this extension could be uploaded and ran without problems and even with some performance in the web version.
A very important feature of NetLogo is the extended set of models that can be run in NetLogo web in the browser but is also directly available in the desk-top version.
Here I describe my experiments with the cellular automaton called The Game of Life. I used the NetLogo implementation NetLogo Life by Uri Wilensky of CCL as a starting point. I loaded the model in the NetLogo desk-top and saved it under a different name. This copies both the code, the user interface and the information so that I can freely experiment with this model.
Changes made to the Uri’s model
- I use a seed for the random number generator. In this way I can repeat and study an interesting simulation and on the other hand force different start setups. Note that (as in the original model) there is a possibility to draw a start setup point-by-point. NB probably the age variable (see last bullet point) needs to be corrected.
- Uri’s model is homogeneous over the whole
world. In the real world some areas are more prone to life then others. Therefore I distinguish threeregimescoded with1(lime colored),2(yellow colored) and0(turquoise colored). In regimes 1 and 2 I will not allow that new life is originated. - Uri’s model is deterministic: he codes an outcome (birth, death or no-change) depending only on the number of neighbours. In the real world things are not that black or white but happen according to a probability distribution, so for each number of neighbours I fix in the code the numbers
$P_d$and$P_b$in the interval$[0-100]$. The code then draws a number$t$from the$U(0,100)$uniform distribution and sets the outcome to ‘death’ if$t \le P_d$and otherwise to ‘birth’ if$t \ge P_b$. Currently the$P_d$and$P_b$values are set in such a way that the behaviour of the new model is the same as that of the original one. - I also keep track of the age of each cell/patch. If the age is very high (currently defined as one hundred thousand) a cell will die.
Adapted interface
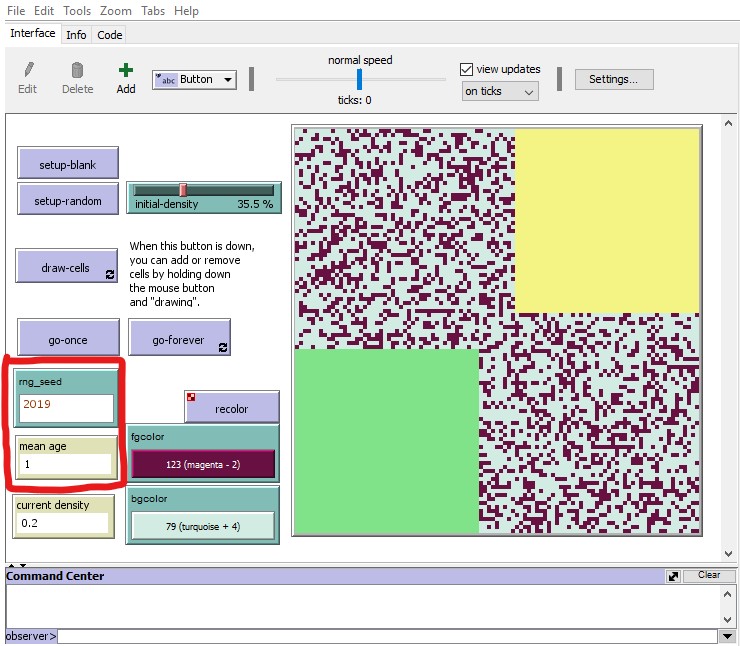
In the image below I show the new interface. In the red box I indicate the rng_seed input box and mean age output box that were added to the original interface. I also show the pattern produced after pressing the setup-random button:
Resulting behaviour
In the following picture I show the first 19 'ticks' of the simulation (for which the display speed was set to slower than normal). The screen capture was done with the open source Windows program ScreenToGif (source on GitHub ).

Full code for model
The full code for this model can be retrieved with the download link.